3月14日，又到了一年一度的\(\pi\)节。以为我会说白色情人节的可以小小失望一下了。像我们这种情人节都只有看别人过的人在白色情人节这天当然是不会有什么庆祝活动的。幸好这天还是\(\pi\)节，也让我们有了庆祝的机会。

3月14是\(\pi\)节的原因应该是不言而喻的。即便你对数学再怎么不了解，稍微念过点书的人都应该知道\(\pi\)的前三位是3.14。但假如让你求出来这个3.14估计就能让很多人望而却步了。而假如让你求出来\(\pi\)的任意位数精度的值估计就能让很多计算机都深感无力了。今天我们就先来探探这个老朋友的究竟，求一求它的值。

要求\(\pi\)的值就要先知道\(\pi\)表示的是什么。\(\pi\)在中国叫圆周率，代表的是平面上圆的周长与直径之比。它是个常数。至于怎么知道它是个常数的，我们放在后面说。我们先假设我们已经证明了它是个常数。既然是个常数就适用于所有的圆。于是我们来考察任意一个圆。

圆的周长与直径的比，既然这样我们要求它的值就直接找个圆测一下周长再测一下直径然后做一下比就行了呗。这是我小学时候的想法。众位能看的出，这个想法果然能配的上我小学生的身份！单纯且直接，简约又清纯。我记得我还想到了测圆周长的方法，弄个轮胎什么的圆形东西，在地上滚一圈，然后测量地上的印迹就是圆的周长。直径就直接一测，然后比出来数值就是\(\pi\)。很傻很天真！显然我那个时候没有无理数这种无理的概念，且不是那种实践派的干事。我只是意淫出来这个悲催的方法并自以为很完美的搞定了\(\pi\)之后就心满意足的不再想这个问题了。现在想想，这果然很符合我的一贯作风。这个方法其实也是一个最直截了当的方法。中国很早就记载了对圆周率这个比值的看法：周三径一。估计用的也就是这个直接量一量的方法。在那个生产力极为落后，人民生活基本靠天的年代，圆周率取个个位3作为近似值估计也够用了。但这明显不是数学家想要的结果。

数学家最大的特点可能就是将实际问题抽象化。当然这种特点也可以解释成一个字：懒！当然是身体懒但脑子不懒。数学家说你弄个圆周率在那量一辈子也量不出来个准确值。于是他们开始把圆周率的问题转化成一个几何问题——割圆术！

再说回我小学意淫圆周率的求法，后来认识了祖冲之老爷子。知道了人家把\(\pi\)算到了小数点后好几位，成了历史名人，名垂千古。貌似那个时候也有了无理数的概念了吧，我这才认识到\(\pi\)其实是个多牛逼的数。小数点后无穷多位，还没有重复，没有规律！这种无理取闹的无理数概念直接给了我幼小的心灵一记沉重的创伤。估计当年毕达哥拉斯听到根号2的存在时心里也是咯噔一下。缓过劲来后我开始想，这个数这么怪，测量是不可能测的准了。因为你可以找一个直径是有理数的圆，它的周长肯定是个无理数，这意味着你肯定直接用尺子神马的是测不出来这个数的。那祖冲之是怎么干的呢？

答案就是算出来的。既然圆这个很完美的没棱没角的混蛋图形没法直接算，那我们就找一些和它很接近的多边形来近似算出它的一些值。于是在一个伟大又基础的数学思想的支持下，我们可以无限逼近\(\pi\)的值。这个思想就是极限。

取圆的任意内接正多边形为研究对象，在已知圆的半径的情况下我们可以算出这个正多边形的周长。当这个正多边形的边数取到无穷大的时候，这个正多边形就逼近圆了。它的周长也就是圆的周长了。光说不练假把式，这个逼近的思想我从初中就接触过，但从来没有亲自演算过。今天我就来用这个算一算。

在算的过程中，我要把以前没细想过的问题都顺便捋一遍。还好都不是啥复杂的问题。

首先说到多边形，我们要用到多边形的内角和公式：（边数-2)*180度， 这个怎么来的呢？

首先来看最简单的多边形—三角形。三角形的内角和是180度。因为取任意三角形的任意一个边，作这条边的一个方向的延长线。再做一条平行线如下图。这时候可以看到相同颜色的角相等。一对是内错角，一对是同位角。于是三角形的三个内角相加等于一个平角，也就是180度。

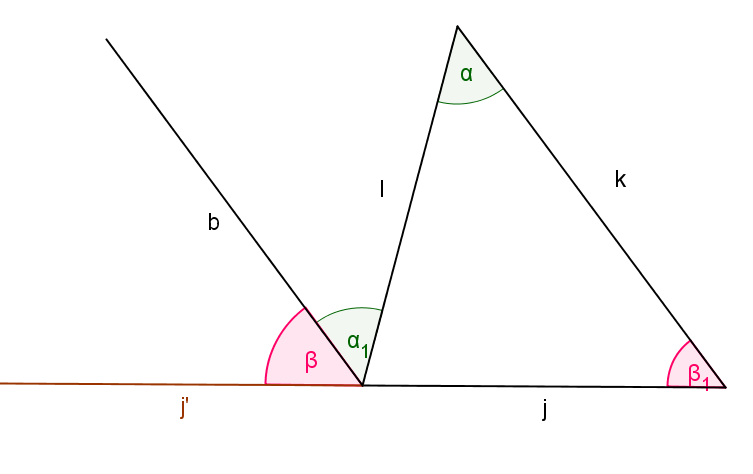
然后来看看任意多边形的内角和。如果你想一下就会发现多边形多一条边其实就是把原有的某条边向外弯折一下。而弯折之后和弯折之前相比内角和相当于多出来一个三角形的内角和。如下图

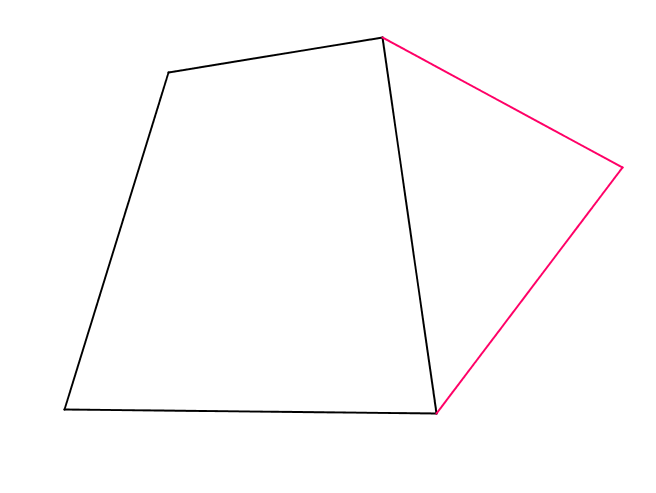
因而多一个边内角和就多了180度。所以\(n\)边形的内角和就是（\(n\)-2）*180度。

知道了多边形的性质我们再来看圆的内接正多边形。

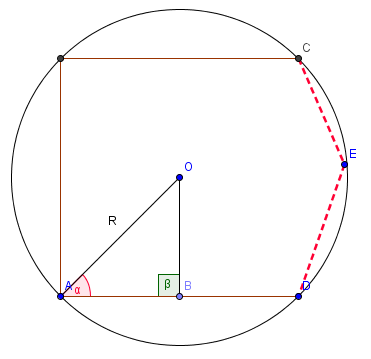
上图是一个半径为\(R\)圆心为\(O\)的圆，园内接一个\(N\)边形。红色的虚线代表了任意多条边。\(OB\)为圆心到多边形一边\(AD\)的垂线。观察三角形\(OAB\)，可求出角\(\alpha\)的大小为\((n-2)\times90^{\circ}/n\)。则\(AB\)的长度为\(R\times\cos\alpha\)。从而可知这个圆内接正\(N\)边形的周长为。

而圆的直径为\(2R\)。则圆周率可以表示为

这个极限值可以用罗必塔法则算出来，在这就不显示步骤过程了。

这个方法在表示多边形的周长的时候用到了三角函数，而极限的相关的知识就是更高端了。我不认为祖冲之老爷子在当时能用这些比较现代且符号系统很规范的方式。但以我现在的想法，我就又很意淫的把割圆术考虑成这个样子了。那么一千多年前的祖冲之是怎么割这个圆的呢？又是用怎样的简单而巧妙的技巧算出圆周率的近似值的呢？

祖冲之其实用的是前人刘徽的方法。只不过自己算的比刘徽精度更高而已。整个割圆术的思想都是三国时期刘徽想出的。他这个思想的精髓就是多边形边数翻倍后的对称性。

他先研究了圆的内接六边形。这是个很明智的选择。虽然从任意正多边形开始研究都是可以的，但正六边形无疑是最简单的一个。因为圆的内接正六边形的边长正好等于半径。这对于古代用筹算计算的数学家们是能简便很多运算的。在下图中，过圆心\(O\)做六边形一边\(AB\)的垂线交\(AB\)于\(P\)，交圆于\(C\)。则三角形\(APO\)和三角形\(APC\)都是直角三角形。运用勾股定理可以得出\(OP\)，再用半径减去\(OP\)得到\(PC\)。再用勾股定理得到\(AC\)也就是圆内接正十二边形的边长。有了这样一步从正六边形边长到正十二边形边长的计算过程我们就能很容易想象用同样的方法从正十二边形得到正二十四边形的边长。以此类推可以得到圆的内接正\(3\times 2^{n}\)边形的边长。而这个过程中只是重复的使用了同一个定理也就是勾股定理。进行的复杂计算也无非就是开平方。这样只要你有足够的耐心和时间，你就能得到任意精度的圆周率数值。

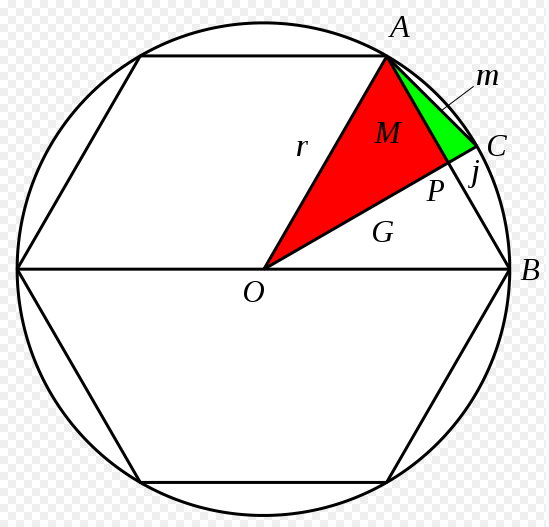
事实上刘徽用的是圆的面积和半径的关系来表示的圆周率。但核心还是刚才所说的算边长的方法。只不过他发现了一些正多边形的面积关系从而能用比较小边数的多边形来达到很大边数的多边形的精度。当然他还想到了用多边形的一些边表示出超出圆的矩形，从而从“外围”来卡圆周率的具体值。他根据此写出了一个圆周率的不等式。而祖冲之正是根据这个不等式算出了\(\pi\)，从而留名千史。当你拿刘徽的这个割圆术和早期西方的一些计算圆周率的方法（比如阿基米德的割圆术）进行相比时你就会发现这个方法的优越性和简洁性。更多关于此方法的介绍可以到此查看。

写到这我们其实还遗留了一个关键性的问题没有解答，那就是\(\pi\)是个永远不变的常数么？

答案当然是肯定的。在众多数学或物理常数中，\(\pi\)应该是受众面最广的一个了。但是在课本没有明确告诉你\(\pi\)是个常数之前，你能意识到这一点么？换句话说你能意识到所有的圆的周长和直径的比值都是一个数么？这似乎是个比较直观的感觉，因为圆这个图形很简单，它就那么几个变量，直径或说半径和周长之间的关系应该是固定不变的。感觉是这么告诉我们的，但是，你能证明它么？古代那些求圆周率的人又是否知道圆周率是个常数呢？

圆周率是个常数，我想这是无法证明的事实，任何常数都是世间规律的一个体现，世界就是这个样子的，所以这些常数就是这样的。你可以假定它是常数，然后通过大量的实践信息来一遍又一遍的印证它是常数这一事实。这就足以了。那么历史上那些数学家假定它是常数了么？当然。不然它们就不会一遍又一遍的去算它的近似值了。比如祖冲之，他在文献中提到他计算的\(\pi\)值的时候有明确说这是个近似值。如果他不认为\(\pi\)是个常数，那么就不会出现近似值这一说法。而且他在用刘徽的割圆术的时候将圆的直径改变了。假如他不认为\(\pi\)是个常数那就会特意注明他求出的近似值是在特定直径下的圆周率近似值。但他没有这么说。而西方的早期数学家在算\(\pi\)值的时候也是如此。他们知道\(\pi\)是个常数，只不过他们很奇怪这个常数为什么永远也算不完。

在现有文献中，最早触及\(\pi\)是个常数的是公元前三百多年的古希腊数学家欧几里得。他在他的伟大著作《几何原本》中证明了两圆面积之比等于直径的平方比。从而就可以推出圆周率是定值的结论。但他没有提及这一点，可能在当时没有意识到这一点。但就在几十年后同样是古希腊数学家阿基米德就明确的表示了\(\pi\)为常数这一观点，并开始计算\(\pi\)的具体值。

我特意去翻了一下《几何原本》，并费了点劲找到了那个证明。不知道是翻译的问题还是古代人和现代人的思维差异，这个短短的证明看的我异常恶心。但最终看懂后还是感觉很有feel的。我在这简洁的表述一下这个证明的过程。

首先欧几里得研究的是圆的面积之比和圆的直径所构成的圆内接正方形的面积之比之间的关系。命题是说这两个比值相等。其实也就是两圆面积之比等于直径的平方比。如下图

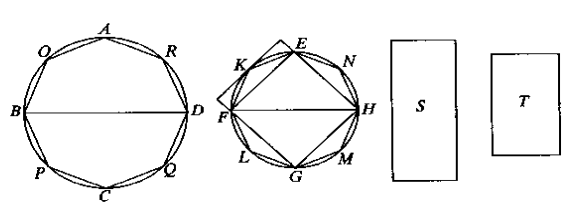
我们首先构造两个圆，圆\(ABCD\)面积大于圆\(EFGH\)。\(BD\)是圆\(ABCD\)的一条直径，而FH是小圆的一条直径。而我们要证明的就是圆\(ABCD\)的面积与圆\(EFGH\)的面积之比等于正方形\(ABCD\)（图中没画边）的面积和正方形\(EFGH\)的面积之比。我们用反证法。假设比值不相等，则正方形\(ABCD\)和正方形\(EFGH\)的比值等于圆\(ABCD\)和一个面积的比值，这个面积要么大于圆\(EFGH\)的面积要么小于圆\(EFGH\)的面积。我们把这个面积设为\(S\)。

现在假设\(S\)小于圆\(EFGH\)的面积。

如果过点\(EFGH\)做一个圆的外接正方形，可以得出圆的内接正方形\(EFGH\)的面积大于圆的面积的一半。\(KLMN\)是所在弧的二等分点。则同理可知三角形\(KFE\),\(NEH\),\(MGH\),\(LFG\)的面积都比所在弓形的面积的一半大。如果再取各弧的中点并做同样的图形，会得到更小的三角形和更小的弓形。并且这些三角形的面积都比所在弓形的面积的一半大。如此分割下去总会有一个时候所有的弓形的面积和要比圆\(EFGH\)的面积和\(S\)的差小。

这是个很明显的结论，因为所有的弓形的面积和随着分割次数的增多在不断减小，而\(S\)是个定值，所以弓形面积和肯定会在某一次分割后小于\(S\)。虽然是个明显的结论，但欧几里得在这里还是证明了一下，并且之前所有说的“三角形面积比所在弓形面积的一半大”这一点都是为了证明这个结论。因为欧几里得在《几何原本》之前的一章证明过“如果有两个量不相等，则从大量中每次减去大于一半的量，若干次后，所余的量必小于较小的量。”这里我认为这个条件可以推广到从大量中减去任何一个大于零的量，结论都成立。这里欧几里得之所以证明了这个应该是正好能用此结论来证明我们现在要证的圆的面积和直径的关系的这个命题。

好，回到我们要证的命题。我们假设分割到这个时候圆\(EFGH\)上\(EN\),\(NH\),\(HM\),\(MG\),\(GL\),\(LF\),\(FK\),\(KE\)所构成的弓形的面积和小于圆\(EFGH\)的面积和\(S\)的差。则余下的多边形\(ENHMGLFK\)的面积要大于\(S\)。因为设弓形面积和为\(A\)，多边形面积为\(B\)，则圆的面积为\(A+B\)，则当\(A<A+B-S\)时，可推出\(B>S\).

现在来看大圆\(ABCD\)，设内接于圆\(ABCD\)的多边形\(AOBPCQDR\)和多边形\(ENHMGLFK\)相似，即边数相等。则此时两个直径构成的内接正方形的面积比就等于这两个多边形的面积比。因为它们都可直接由直径和边数确定而和圆无关。而根据我们的假设，这两个正方形的面积之比等于圆\(ABCD\)和\(S\)的面积比。因而圆\(ABCD\)和\(S\)的面积比等于多边形\(AOBPCQDR\)和多边形\(ENHMGLFK\)的面积之比。写成比例式之后换一下位置就能得到圆\(ABCD\)和其内接多边形\(AOBPCQDR\)的面积之比等于\(S\)和多边形\(ENHMGLFK\)的面积之比（绕不清的可以自己写写试试）。此时重点来了，因为圆\(ABCD\)的面积肯定比内接多边形的面积大，所以由刚才得出的比例关系可知\(S\)的面积要比多边形\(ENHMGLFK\)的面积大! 由此得出矛盾，假设不成立。

现在我们假设第二种情况：\(S\)大于圆\(EFGH\)的面积。

此时正方形\(EFGH\)和正方形\(ABCD\)的面积比等于\(S\)和圆\(ABCD\)的面积比，这个比值也就等于圆\(EFGH\)和一个小于圆\(ABCD\)的面积的面积比。如果设这个比圆\(ABCD\)的面积小的面积为\(T\)的话，这个比例的等式就是

正方形\(EFGH\)：正方形\(ABCD=S\)：圆\(ABCD=\)圆\(EFGH\): \(T\)

此时我们发现\(T\)就相当于前一个假设中的\(S\)的地位。由于前一个假设不成立，这个假设也是不成立的。

由此我们推出\(S\)只能等于圆\(EFGH\)。即两圆面积之比等于直径的平方比

我们可以看出这个证明过程中是完全不涉及圆的面积公式的，也就是说是完全不用提圆的直径和面积之间的具体关系的。换句话说这个过程是不用涉及圆周率这个概念的。然而其结论确实是可以得出圆周率\(\pi\)是个常数这一事实。想到这些我只能深深发表一个感慨，欧几里得，你太牛逼了！

说完了\(\pi\)是个常数，我们再回到\(\pi\)的具体值的问题上来。话说古今中外无数数学痴汉都想把\(\pi\)的真面目彻底揭露出来，他们有的甚至穷极一生来计算\(\pi\)的数值。比如历史上最马拉松式的计算之一是德国的Ludolph Van Ceulen，他几乎耗尽了一生的时间，计算到圆的内接正262边形，于1609年得到了圆周率的35位精度值，以至于圆周率在德国被称为Ludolph数。还有一个是英国的威廉·山克斯，他耗费了15年的光阴，在1874年算出了圆周率的小数点后707位，并将其刻在了墓碑上作为一生的荣誉。可惜，后人发现，他从第528位开始就算错了。虽然悲剧了，但他坚持不懈敢于拼搏的献身精神依然不值得我们当代这些抱着计算机上学的学生所学习。

以前的人这么废寝忘食无休无止的计算\(\pi\)，无非是想知道这孙子到底有没有完！到底会不会到某一位开始出现循环。真正的数学家是不喜欢做机械式的苦力运算的。他们更喜欢从本质上解决问题。随着关于\(\pi\)的多种无穷级数和连分式的表达的出现，人们计算\(\pi\)的效率越来越高了。但数学家还是不满意这种没有止境的运算。如果\(\pi\)是个无理数的话，你是永远也无法通过计算来证明它是无理数的。因为你永远也不可能把它算完。而且大量的计算出的数据显示\(\pi\)大概其就是个无理数了。那么好了，挑战数学家的时候到了，\(\pi\)是个实数是可以肯定的了，既然是个实数那它不是无理数就是有理数。不管是哪个，请证明吧！

于是1761年德国数学家Lambert证明了圆周率是无理数，1882年Lindemann证明了圆周率是超越数。

这下\(\pi\)的面纱被彻底揭开了。\(\pi\)这个朴实又神秘，清纯又富有深度的科学界最本质的一个常数不负众望的穿着一身华丽的无理数外衣站在了世人的面前，它的周身散发着象征着高贵的超越数光环。而由它构成的图形圆也可以名不副实的被称为最完美的图形。为什么我很完美？因为我富有深度。

关于\(\pi\)是无理数和超越数的证明，我们留在明年的\(\pi\)节吧。我并不希望像弘扬传动节日一样把\(\pi\)节宣传的多值得庆祝。事实上我们只是在自娱自乐中找到一点纪念与传承的感觉。这就足以了。

参考资料：

维基百科：割圆术（刘徽）

台师大数学系洪万生教授：魅力无穷的祖率

杨嘉慧：从\(\pi\)遇见人类数学史

欧几里得：《几何原本》（兰纪正 朱恩宽译，陕西科学技术出版社）

P.S. 我前一篇发的猜题看图的文章里最后一道题是个找规律题。题目很简洁我不妨在这再写一遍

3,31,314159,?

看到这个一般都能想到和\(\pi\)有关。没错，这就是截取了\(\pi\)的某一位后写成的整数。那么是按什么规律截取的呢？这三个数有什么共同点呢？3和31都是很简单的数，而如果你查一下314159这个数你会发现它是个质数。而3和31也都是质数。所以这个数列的规律就出现了。那么查一下就可以找到下一个数了。

我写这个题目的时候其实并不知道这个数列的每一项是什么。我只是有这么个想法然后用WolframAlpha一个一个去试\(\pi\)的数找到的第三和第四个数。第三个只有6位还是很好找的，第四个就变成38位了，着实让我找了一会。我当时都不确定自己能不能找到这个数，比如如果这个数是一百多位我肯定是一时半会试不出来的。在我试到第38位时发现是个质数的时候真的小激动了一下。然后仔细核对了两遍确定自己没有写错。现在再来看这个数列时我试着在网上搜了一下，发现果真这个数列是早就有人研究过的。在这里你可以看到关于它的更多介绍。

P.S.2 本着节日必有福利的二次元思想，我当然不会忘了在最后给大家发糖吃！这个视频是圆周率版《恋愛サーキュレーション》。声音超像原版哦！一共唱到\(\pi\)的小数点后456位哦！千石抚子哦！