昨天在MATRIX67神牛的BLOG上看了一篇关于超级幂的东西。后来不知道怎么不知不觉就开始想考虑\(y=x^{x}\)这个函数的问题了。
上高中的时候其实想过这个问题。也似乎明白这个函数的图开始在\([0,1]\)这个区间上的时候会有一些下降的趋势,但是因为能力有限,没有学到导数的一些高级的求法,所以也就没有再探求下去。
又提起来这个函数,我觉得要稍稍搞一下了。于是用几何画板花了以下这个\(f(x)=x^{x}\)的图:
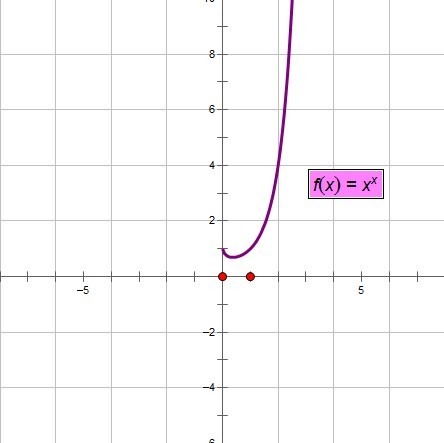
由于在负数的里面有不合法的地方,所以在图像上就没有表示,实际上底数上还是应该有一些离散的点的,至少我这么意味吧。
正如这个图像所知的,是有一个最低点的。一开始我并没有想到怎么去求。于是就开始回忆,后来回忆到似乎可以用数列的方法来逼近最低点。但是发现是一个恒等式:
\[x^{x}=(x+m)^{(x+m)}; (0\leq m\leq 1)\]然后我就开始了白痴的两边用自然对数去变形,变形后整理发现出现了这样的形式:
\[\frac{x}{x+m}=\frac{\ln(x+m)}{\ln x} (0\leq m\leq 1)\]这明显就是一个恒等式。这时我才意识到不太对。于是我就开始用计算机来逼近这个东西,最后发现在0.36~0.37之间。本来就想研究到这里算了,后来发现了这个页面:
http://www.analyzemath.com/calculus/Differentiation/first_derivative.html
这个页面是讲\(y=x^{x}\)的求导方法。我略略的一看,哎呀~这不就是当年的求导方法里面的一个最常用的方法么?(顺便提一下上面的网站,是一个解决数学问题的英文站)
于是产生了下面的运算:
\[x>0; y=x^{x}\]对等式两边用自然对数变形:
\[\ln y=x\ln x\]两边同时求导:
\[\frac{dx}{dy}\times\frac{1}{y}=\ln x+1\]因为\(y=x^{x}\);
所以:
\[\frac{dx}{dy}=(\ln x+1)\times(x^{x})\]此时使\(\ln x+1=0\)即可使导数等于0,即最低点位置。所以求的\(x=\frac{1}{e}\);
其实这篇BLOG比较无聊,主要是这种方法觉得应该拿出来讲一讲。在求最低点走投无路的时候,不妨拿起来看一看。。